One morning I was standing in a queue in my local bakery, and I’ve seen a woman buying one of those small quasi-pizzas. Pizzas ~20cm in diameter. Immediately I thought about how profitable it is when compared to the full-size 42cm pizza. Since the area of a larger pizza is 4 times bigger, of course, it’s not worth buying smaller pizzas.
Then I thought about fitting smaller pizzas inside the bigger one. But first let’s think about filling a square with smaller squares.

Pizzas packed in pizza
Filling a square
Suppose you have a square with side of length $a$. If you double the side length, you quadruple the area. And then you can easily fit small squares into the bigger one.
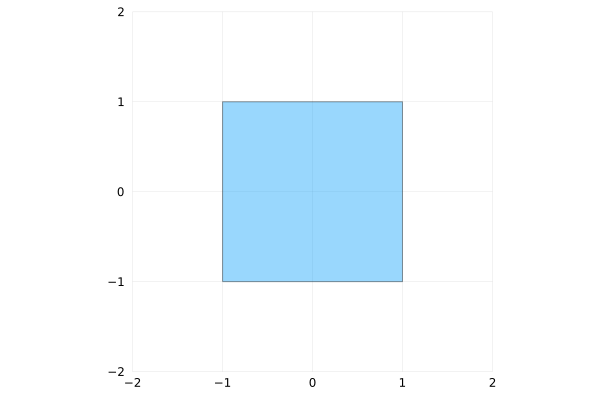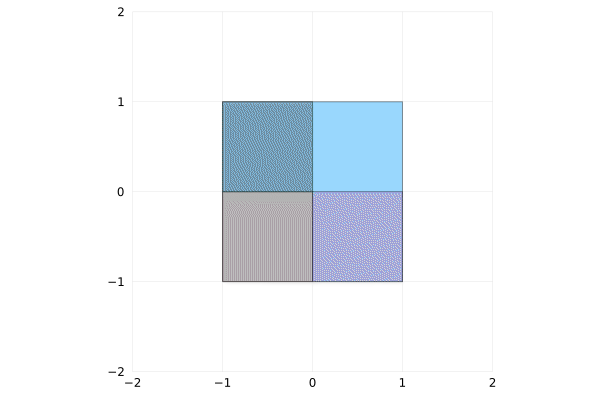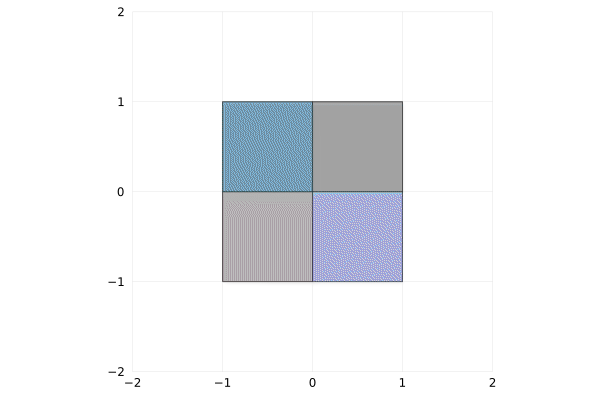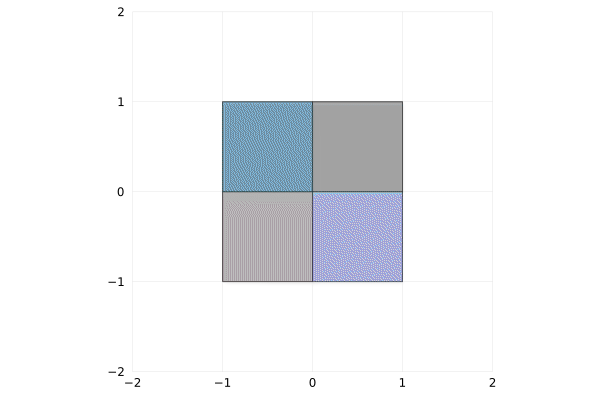
This example is trivial, but how about doubling the area instead of side length?
Since the area of a square is $A = a^2$, if we want to double the area, our side will be:
$$
a_{\text{half}} = \sqrt{2 A} = \sqrt{2 a^2} = \sqrt{2}a.
$$
Fortunately it’s easy to create segment of length $\sqrt{2}a$, it’s the diagonal of a square with side $a$.
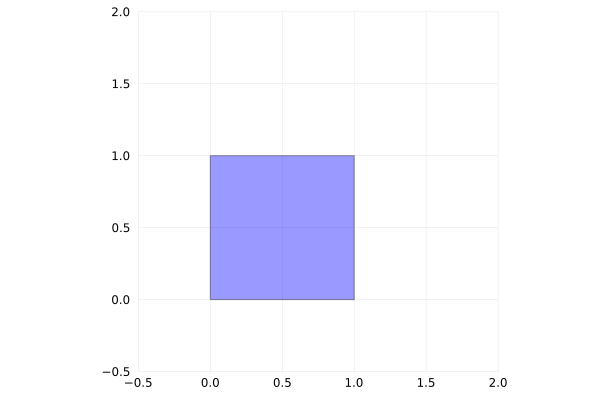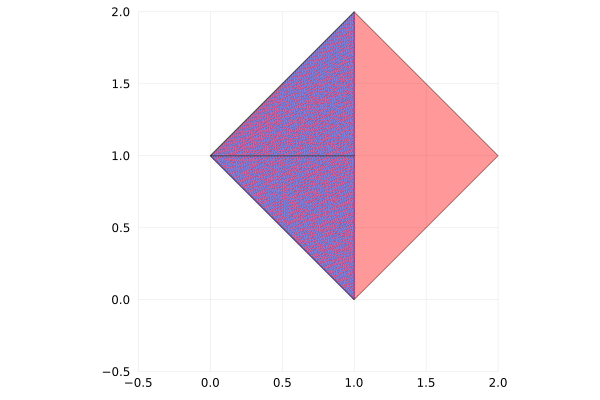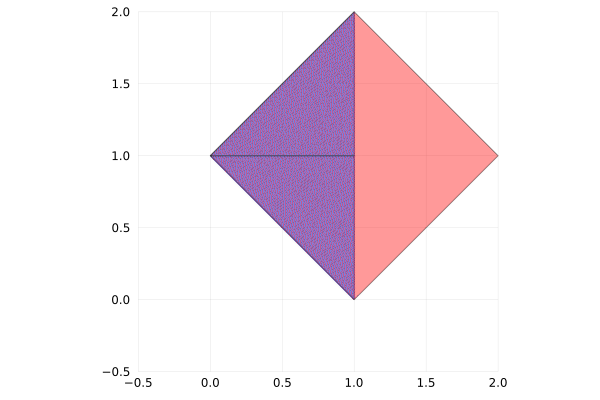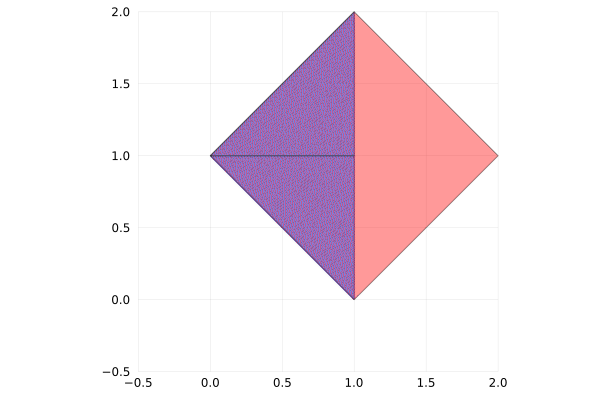
Filling a circle
Filling a circle is a different thing. Let’s consider the area of pizza with radius $r_1=1$ and with radius $r_2=2$. Using a highschool equation for area $A = \pi r^2$, we find out that: $$A_1 = \pi 1^2 = \pi,$$ $$A_2 = \pi 2^2 = \pi \cdot 4 = 4 \pi,$$ $$A_2 = 4 A_1.$$ So we clearly see that we should be able to fit exactly 4 smaller pizzas into the bigger one. But now let’s try to plot how it could look like:
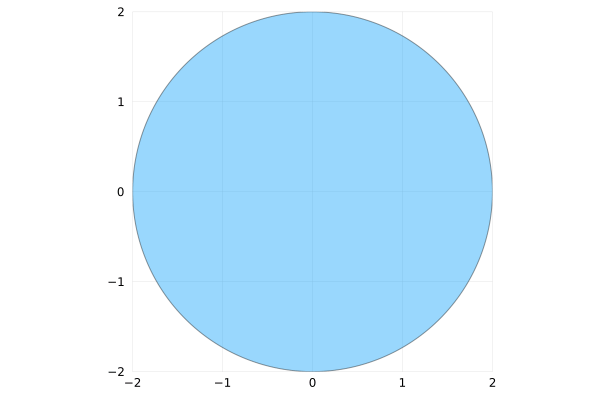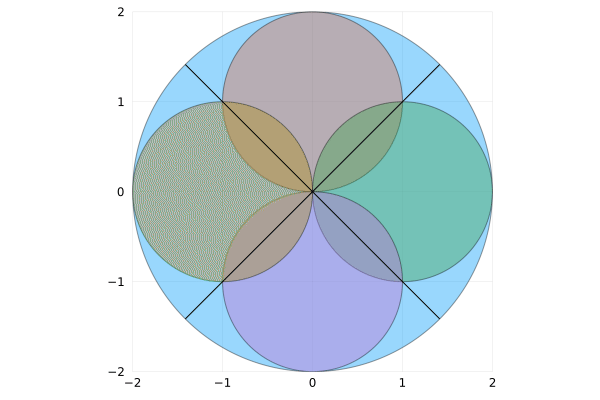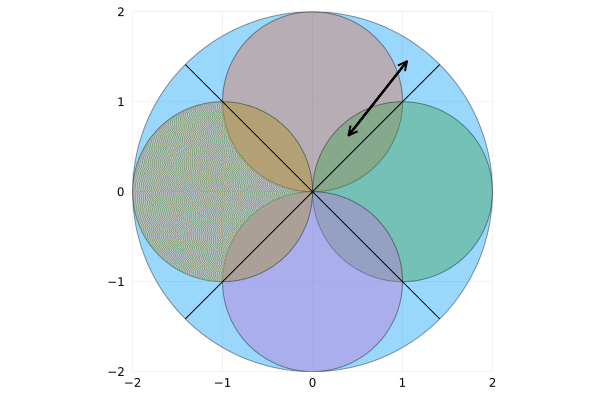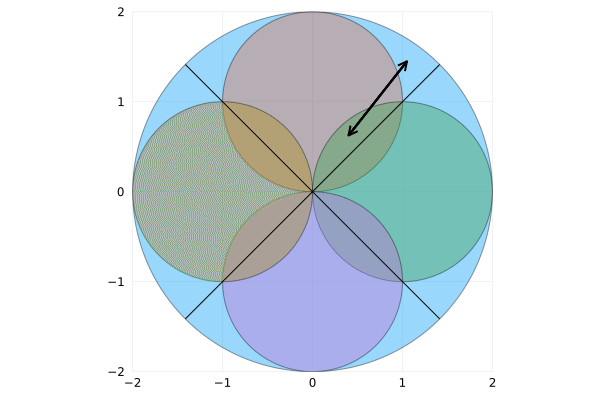
Look how strange it is. Fields connected with an arrow have exactly the same area! That’s because there are exactly 8 areas near the circle center and 8 near the edges.
And for a complete picture, let’s see how circles with radiuses $r_1 = \sqrt{2}$ and $r_2 = 2$ look like when you try to fit them inside the other:
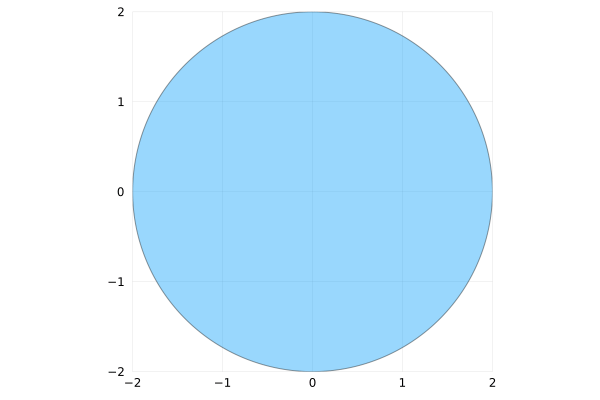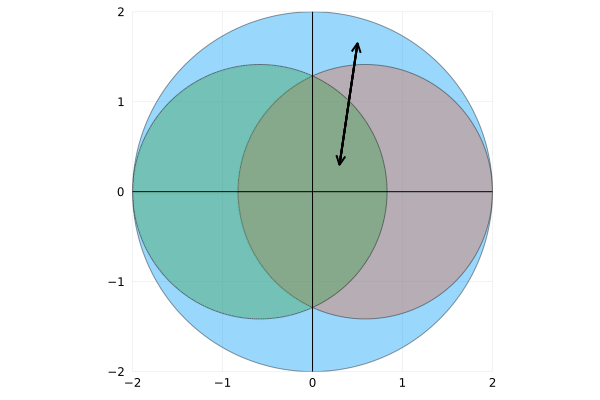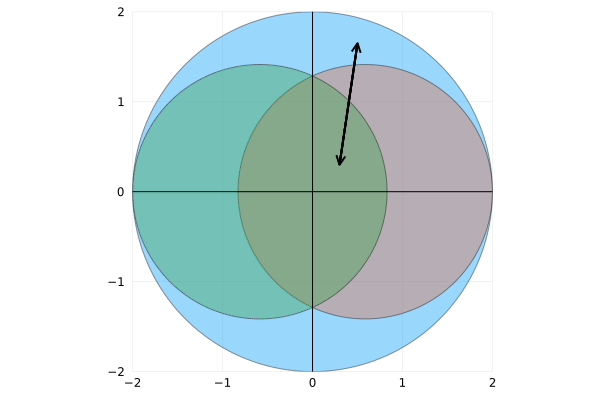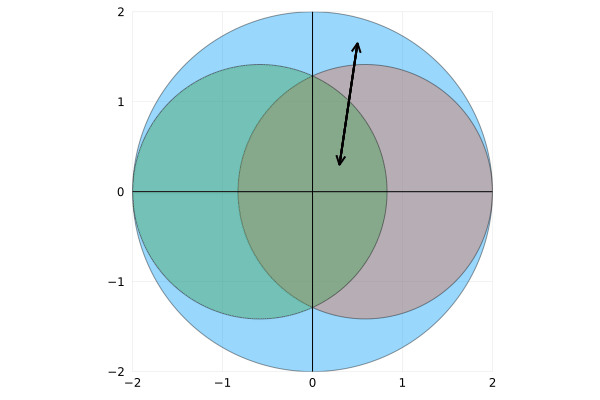 I think it’s remarkable to think of numerical value of $\sqrt{2}$.
Pretty often in restaurant you might think how much larger pizza should be to have a double area.
This table with common pizza sizes should help you make a data driven decision next time :)
I think it’s remarkable to think of numerical value of $\sqrt{2}$.
Pretty often in restaurant you might think how much larger pizza should be to have a double area.
This table with common pizza sizes should help you make a data driven decision next time :)
| Smaller pizza diameter | Pizza of double area diameter |
|---|---|
| 21.5 | 30.4 |
| 30.0 | 42.4 |
| 38.0 | 53.7 |
| 42.4 | 60.0 |
Summary
That’s it for today. Even though circles are all around us, they examine interesting features that you can think about for your whole life… Use the table next time you visit your favorite pizza restaurant.
Expect the post on packing circles in ⬤ (recreating the first image) soon!
If you liked it, please share my blog with friends that might be interested in such posts :)
Code used to generate all images is available at GitHub.